Consideremos el siguiente problema:
Tenemos los siguientes datos y definiciones:
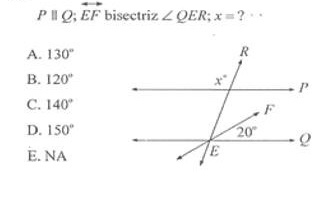
A) Las rectas P y Q son paralelas;
B) La recta R se interseca con las rectas P y Q;
C) La intersección entre R y P forma dos ángulos, uno de los cuales es x, cuya medida se nos pide determinar;
D) La semirrecta EF es la bisectriz del ángulo QER, formado este último por la intersección de R y Q en el punto E;
E) Llamamos «bisectriz» a la semirrecta que pasa por el vértice de un ángulo y lo divide en dos partes iguales;
F) Llamamos «congruentes» a dos ángulos de igual medida.
G) Llamamos «suplemento de un ángulo» a la medida que le falta para formar un ángulo llano;
H) Un «ángulo llano» mide 180 grados;
I) Llamamos «suplementarios» a los ángulos cuya suma es igual a 180 grados.
A la luz de todo lo anterior, nuestro problema se resuelve de la siguiente manera:
Solución
(1) Dado que EF es la bisectriz del ángulo QER, eso por definición significa que lo parte en dos ángulos iguales. El problema dice que uno de esos ángulos mide 20. Por lo tanto, el otro también mide 20. Luego, QER mide 40.
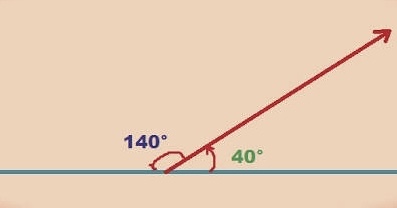
(2) La recta Q se interseca con la recta R en el punto E. Tal intersección genera, como vimos en (1), un ángulo de 40 grados. Luego, su suplemento es de 140.
(3) Puesto que la recta P es <paralela> a la recta Q y también se interseca con R, el ángulo x generado por los ángulos generados por la intesección deben ser congruentes con los señalados en (1) y (2).
(4) Por lo tanto, x debe ser congruente con el ángulo suplementario de QER. Puesto que tal ángulo mide 140, entonces x=140.
La respuesta es C.
