Si al aproximar x lo suficientemente cerca de un numero a, su imagen – f(x) – se aproxima a un número L, entonces el limite cuando x tiende al número a es L. Esto lo denotamos por:
Que se lee: «Límite de f(x) cuando x tiende a a es igual a L«.
Por ejemplo, dada la función f(x)= x2 + 1, el límite de f(x) cuando x tiende a 2 es 5. Así, el comportamiento de esta función cuando x se acerca a 2 viene dado por la siguiente tabla de valores y su correspondiente gráfica:
Como se ve, conforme x tiende a a=2, f(x) se aproxima a L=5. Este segundo número es el límite de la función.
Así, por límite se entiende formalmente lo siguiente:
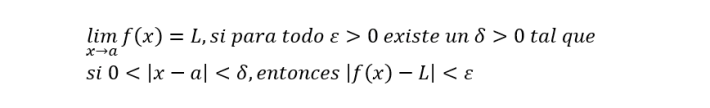
Algunos teoremas relativos a los límites compilados en Aguilar, et al (2009: 1168) para f(x) y g(x) – funciones – y para c y n – constante y número real, respectivamente – son:
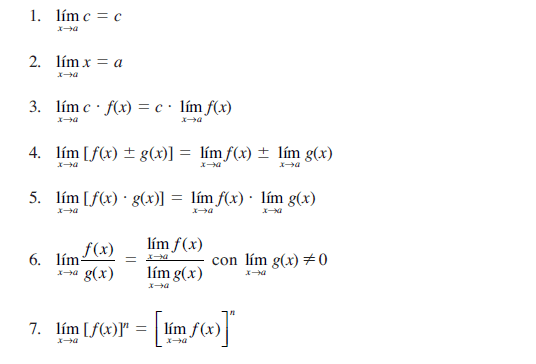
Por último, decimos que una función f(x) es continua en un punto x0 si y sólo si
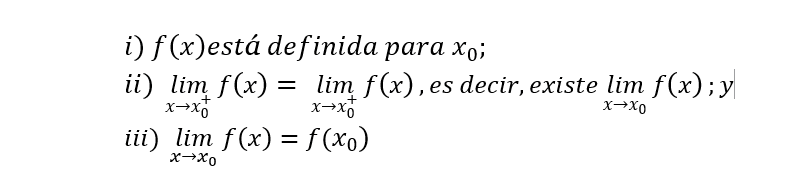
Una función es continua en un intervalo (abierto o cerrado), si es continua en todos los puntos del intervalo.
Fuentes:
Aguilar, A., et al (2009). Matemáticas Simplificadas. México: Pearson.
Proposiciones Simples 