1) Introducción

El objetivo de estas líneas es desarrollar una breve introducción a la que posiblemente sea la más elemental de las aplicaciones del cálculo integral, pero en ella subyace el corazón conceptual de las intuiciones matemáticas a las que el cálculo brinda rigor y estructura definida. Me refiero, pues, a la utilización del cálculo integral como herramienta matemática para la determinación del área de formas geométricas irregulares. Esta aplicación tiene uso patente para la determinación del tamaño de la superficie de terrenos, heredades o fincas.

2) ¿Por qué es importante esta aplicación del cálculo integral?

La tenencia de la tierra es un asunto ubicuo en la cultura humana y la historia del desarrollo de las civilizaciones. Es un fenómeno de orden social, económico/comercial, político, jurídico y, naturalmente, un asunto también matemático.

Las tierras con frecuencia están a la orilla de cuerpos de agua como lagunas o ríos. En particular, los ríos, representan un caso de interés pues en ellos ocurre un fenómeno geológico de singular relevancia en el ciclo de la roca (que no es sino el “ciclo de la tierra” misma): la meteorización y erosión de la tierra. El caudal del río hace fricción con las rocas que conforman el suelo y, por un lado, generan cambios físicos en la roca (meteorización física) y arrastran sedimentos (erosión).

En la tradición jurídica, el arrastre de sedimentos por los ríos – bien sea por su caudal “habitual” o cuando estos se desbordan – es un fenómeno que ha sido causa por siglos de controversias en el ámbito del derecho civil (que es la rama del derecho que en general se ocupa de la propiedad y posesión de las tierras). En el caso de muchas de las tradiciones del derecho civil vigentes en nuestro país, se le llama a este fenómeno “aluvión”, que es cuando la erosión ocasionada por los caudales de los ríos o sus crecientes en épocas de inundación provoca cambios importantes en la extensión – esto es, el área – de los terrenos.

El aumento o disminución del tamaño de los terrenos a causa del aluvión da lugar a un fenómeno jurídico de accesión a la propiedad de las tierras transportadas. Así, en términos de – por ejemplo – el Código Civil para el Estado de Tabasco, se define esta situación del siguiente modo:

“ARTÍCULO 1009.- Concepto. La accesión es un medio de adquirir la propiedad, mediante la unión o incorporación de una cosa que se reputa accesoria a otra que se denomina principal.

Por virtud de la misma, la propiedad de los bienes da derecho a adquirir todo lo que se les une o incorpora, natural o artificialmente, conforme a los siguientes principios:

 I.- Lo accesorio sigue la suerte de lo principal; y

 II.- Nadie puede enriquecerse a costa de otro.

(…)

ARTÍCULO 1018.- Qué pertenece al dueño por accesión. Todo lo que se une o se incorpore a una cosa, lo edificado, plantado y sembrado, y lo preparado o mejorado en terreno o finca de propiedad ajena, pertenece al dueño del terreno o finca, con sujeción a lo que se dispone en los artículos siguientes.

(…)

ARTÍCULO 1031.- Aluvión. El acrecentamiento que por aluvión reciben las heredades confinantes, con corriente de agua, pertenece a los dueños de las riberas en que el aluvión se deposite.”

En la siguiente imagen, podemos observar terrenos a las orillas del Río Carrizal en el municipio de Centro Tabasco. Las modificaciones a las superficies de las tierras en esa zona están sujetas a las disposiciones legales antes señaladas.

El problema en cuestión, por elemental que parezca, se trata de un problema con una tradición histórica monumental que se remonta hasta los romanos y, más atrás aún, a los egipcios quienes sabemos que hicieron algunos de los primeros desarrollos de la geometría justamente para abordar el problema de la división de la tierra en las laderas del Río Nilo.

El tema aquí de nuestro interés no es tanto el tratamiento del fenómeno del aluvión, sino hablar sobre la importancia de poseer una herramienta fiable para el cálculo de las superficies de los terrenos. Es importante contar con una herramienta así, en general, porque queremos certeza y precisión sobre las dimensiones de los bienes raíces (pues de ello depende su valor comercial, el pago de impuestos, los espacios para la construcción, etc.). Así mismo, es importante esta herramienta en el caso particular de los terrenos que se ven afectados por fenómenos como el aluvión, pues esto ocasiona que el cálculo de su superficie sea algo que se tiene que hacer con mayor frecuencia que en el resto de los casos y, de nuevo, deseamos hacerlo con certeza y precisión, ambos valores que informan el espíritu del razonamiento matemático.

El valor de la aplicación del cálculo integral a esta tarea radica, entonces, no en su grado de sofisticación matemática – pues, como veremos, es bastante elemental – sino en la transdisciplinariedad del problema que aborda. Hoy en día es un tema que tenemos plenamente comprendido: comprendemos lo que ocurre a nivel geológico, físico, legal, económico, etc. Contamos, además, con una herramienta matemática ampliamente estudiada para abordar con solvencia este fenómeno con significación social y natural. Pero antes que verlo como algo sobre lo que “ya no hay nada que decir”, yo modestamente pienso que es un ejemplo perfecto de cómo la matemática se aplica con éxito en la vida humana para la solución de problemas. Esta es la razón por la que lo he elegido.

3) Planteamiento de la aplicación

Supongamos que un río pasa a espaldas de un terreno formando una curva de la forma f(x)=x^2 con la parte frontal del terreno (que es recta). Si queremos saber el área del espacio que hay debajo de dicha curva, la aproximación fundamental es dividir ese espacio en formas geométricas familiares cuyas áreas sabemos calcular sin grandes dificultades, por ejemplo, en rectángulos.

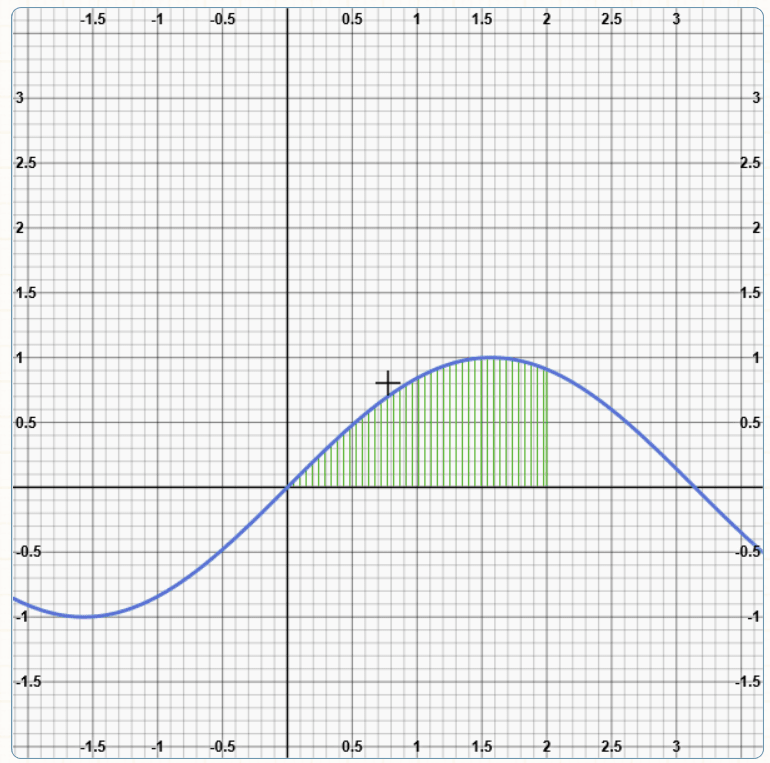
Imaginemos que el terreno en cuestión es el área entre la curva f(x)=x^2, el eje x y las rectas x=0 y x=2. Observémoslo en la siguiente gráfica:

Como sabemos, podemos hacer el cálculo por aproximación mediante la suma del área de rectángulos o cuadrados. Esto es lo que llamamos Suma de Riemann. Lo que nos enseña dicha suma es que, entre más pequeños sean los rectángulos o cuadrados, más precisa será la aproximación al área de la superficie bajo la curva.

Así, asistidos del concepto de límite, si hacemos esos rectángulos infinitesimalmente pequeños (entre más aproximemos su base a 0, sin llegar a serlo), más preciso será el cálculo. Luego, el área del espacio debajo de la curva se define, en general, por el límite

Pero sabemos también que el límite cuando “x” tiene a infinito de la función en cuestión es igual a la integral definida para la función, cuyo intervalo viene dado por las rectas que encierran la superficie a calcular. Esto es:

Este paso de la intuición expresada en las Sumas de Riemann a la noción de integral definida es, en mi personal punto de vista, el núcleo conceptual del cálculo integral. Es la idea que de manera más clara y elemental captura el concepto mismo del cálculo y su aplicabilidad.

4) Desarrollo

En concreto, para el caso hipotético que hemos planteado aquí, las rectas que establecen el intervalo pertinente son x=0 y x=2. Luego, la integral que queremos resolver es

Pues, como dijimos, la curva viene dada por f(x)= x^2.

Para comenzar nuestra solución, resolveremos la integral indefinida:

Esta es una integral directa…

Una vez resulta la integral, procedemos a evaluarla en el intervalo [0, 2] aplicando el teorema fundamental del cálculo

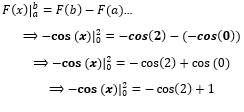
5) Solución

El área de la superficie debajo de la curva f(x)=x² , entre el eje x y las rectas es aproximadamente de 1.41615 u²

6) Conclusiones

El Cálculo es una de las ramas de las matemáticas con mayor número de aplicaciones prácticas. Dichas aplicaciones abarcan una cantidad amplísima de ámbitos del saber humano que van desde la física, la química y las llamadas “geociencias”, hasta las ciencias económicas y sociales. El cálculo integral permite el desarrollo de modelos matemáticos aplicables a tareas o desafíos en la industria, el comercio y las ciencias. Permite la cuantificación de los problemas para obtener conclusiones revestidas de rigor matemático, soluciones que – a su vez – facilitan la comprensión de los fenómenos modelados, posibilitando la predicción de su comportamiento. Esto le convierte en una pieza fundamental para el desarrollo del conocimiento humano.

7) Fuentes de consulta

• Arnaldez, R., et al (1988). Las antiguas ciencias del Oriente. Barcelona: Ediciones Orbis S.A
• Código Civil para el Estado de Tabasco. Periódico Oficial del Estado. Tabasco, 5 de julio de 2017.
• DCEIT (s.f.) “Unidad I. Integrales”. Contenidos en línea para la asignatura Cálculo Integral. Universidad Abierta y a Distancia de México.
• Stewart, J. (2012). Cálculo de una Variable. México: Cengage Learning, 7ma. Ed., pp. 354 y ss.
• Tarbuck, E. y Lutgens, F. (2005). Ciencias de la Tierra. Una introducción a la geologái física. Madrid: Pearson, 8a. Ed.